Sekvenser och mönsterFibonacci-nummer
Föreställ dig att du har fått ett par babykaniner, en hane och en kvinna. De är väldigt speciella kaniner, eftersom de aldrig dör, och den kvinnliga föder ett nytt par kaniner exakt en gång i månaden (alltid ett par manliga och kvinnliga par).




















Under följande månad skulle du ha 13 par kaniner: de åtta från föregående månad, plus 5 nya uppsättningar av spädbarn. Kan du upptäcka ett mönster i den här sekvensen?
Antalet kaniner under en viss månad är
Kan du beräkna antalet kaniner efter några månader till?
1, 1, 2, 3, 5, 8,
Så efter 12 månader har du 144 par kaniner!
Denna sekvens av nummer kallas
När Fibonacci föddes 1175 använde de flesta människor i Europa fortfarande det
När han återvände till Italien skrev Fibonacci en bok som heter Liber Abaci (latin för ”The Book of Calculations”), där han först introducerade de nya arabiska siffrorna för europeiska handlare. De var en omedelbar framgång - och vi använder dem fortfarande idag.
På en av sidorna i sin bok undersökte han också kaninernas avelsmönster - det är därför Fibonacci-numren fick sitt namn efter honom.
Pages from Fibonacci’s Liber Abaci
Naturligtvis är Fibonacci-siffrorna inte hur kaniner faktiskt befolkar i verkliga livet. Kaniner har inte exakt en manlig och en kvinnlig avkom varje månad, och vi har inte redovisat att kaniner dör så småningom.
Men det visar sig att det finns många andra platser i naturen där Fibonacci-nummer gör visas: till exempel spiralerna i växter. Kan du räkna hur många spiraler det finns i varje riktning?
Denna kotte har
Denna solros har 34 medurs spiraler och 55 moturs spiraler.
I båda fallen är antalet spiraler i följd Fibonacci-nummer. Detsamma gäller för många andra växter: nästa gång du går ut, räkna antalet kronblad i en blomma eller antalet löv på en stjälk. Mycket ofta kommer du att upptäcka att det är Fibonacci-nummer!
Naturligtvis är detta inte bara en slump. Det finns ett viktigt skäl till att naturen gillar Fibonacci-sekvensen, som du lär dig mer om senare.
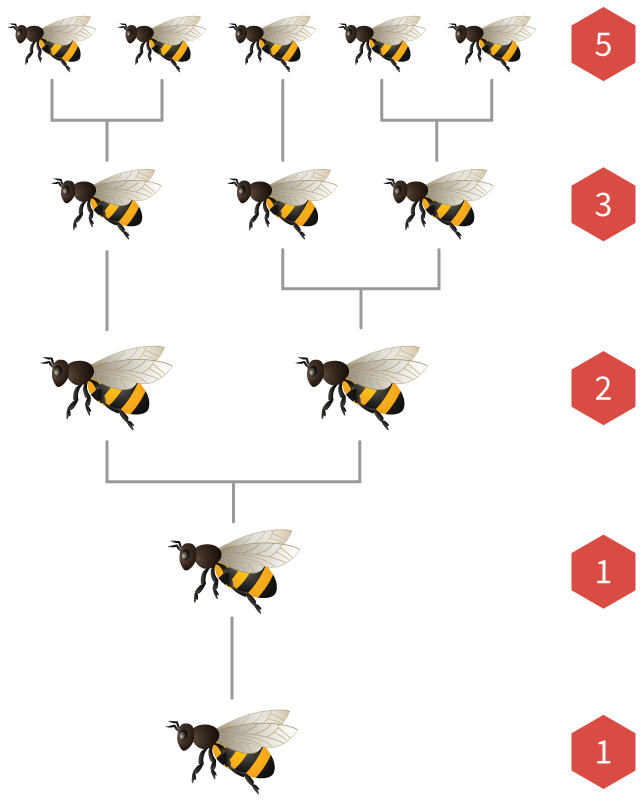
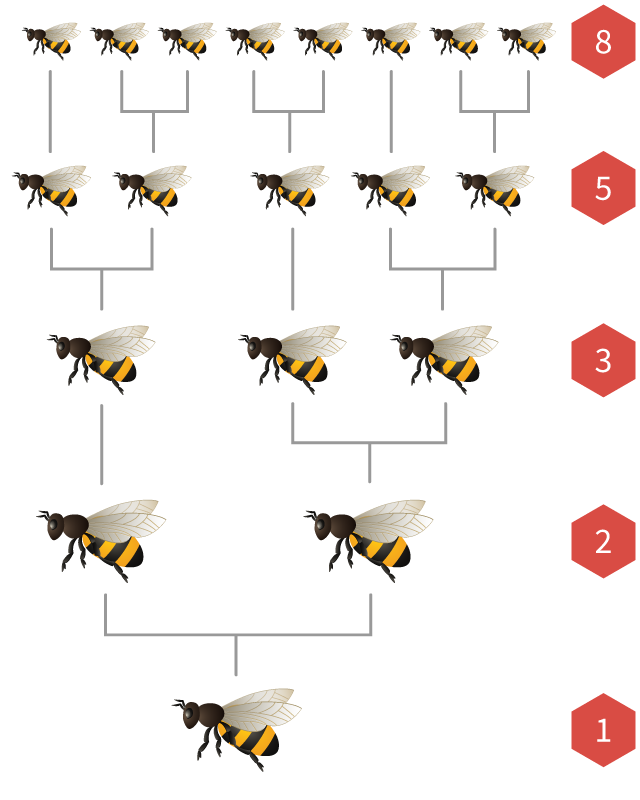
Fibonacci-nummer visas också i populationerna av honungsbin.
I varje bi-koloni finns en drottning som lägger många ägg. Om ett ägg befruktas av ett manbi, kläcks det till ett kvinnligt bi. Om den inte befruktas kläcks den i en hane bi (kallas drönare).
Detta betyder att kvinnliga bin har
Om vi ritar ett bi, är antalet föräldrar, morföräldrar, morföräldrar och tidigare generationer alltid Fibonacci-nummer!
Ibland matas unga kvinnliga bin med särskild mat som kallas "kunglig gelé". I så fall förvandlas de till drottningar och flyger iväg för att starta en ny bikupa.
Golden Ratio
Precis som
Vid varje steg bildar rutorna en större rektangel. Dess bredd och höjd är alltid två Fibonacci-nummer i följd. Rektangelns bildförhållande är förhållandet mellan dess bredd och höjd:
Lägg märke till hur, när vi lägger till fler och fler rutor, verkar bildförhållandet närma sig och närmare ett specifikt nummer runt 1,6. Detta nummer kallas
Många tror att det gyllene förhållandet är särskilt estetiskt tilltalande. Det är därför det ofta används av konstnärer och arkitekter - som i dessa två exempel:

Den grekiska skulptören Phidias sägs ha använt Golden-förhållandet när han utformade Parthenon i Aten. Den första bokstaven i hans namn,

Sacrament of the Last Supper, av den spanska konstnären Salvador Dalí, är en av många målningar i det gyllene förhållandet. I bakgrunden kan du också se en stor
Vi kan ungefärligt gyllene förhållandet genom att
Det visar sig emellertid att det exakta värdet för
Fibonacci-spiraler
Det gyllene förhållandet förklarar varför Fibonacci-siffror visas i naturen, som solrosen och kotten som du såg i början av detta avsnitt.
Båda dessa växter växer utåt från deras centrum (en del av växten som kallas meristem). När nya frön, löv eller kronblad läggs, skjuter de de befintliga längre utåt.
Flytta reglaget till höger för att visualisera hur en växt växer. Lägg märke till hur varje blad läggs till med en annan rotation än det föregående. Vinkeln mellan två på varandra följande blad är alltid densamma.
Det är viktigt för blommor att välja en lämplig vinkel: bladen eller frönna måste vara ungefär lika fördelade så att de får den största mängden solljus och näringsämnen. I diagrammet nedan kan du undersöka hur en solros kan se ut med olika vinklar mellan dess frön:
Du kommer kanske att komma ihåg från ovan att förhållandena mellan på varandra följande Fibonacci-nummer kommer närmare och närmare det gyllene förhållandet - och det är därför, om du räknar antalet spiraler i en växt, kommer du ofta att hitta ett Fibonacci-nummer.
Det är viktigt att komma ihåg att naturen inte vet om Fibonacci-nummer. Naturen kan inte lösa ekvationer för att beräkna det gyllene förhållandet - men under miljoner år hade växter god tid att prova olika vinklar och upptäcka det bästa.
Växter och djur vill alltid växa på det mest effektiva sättet, och det är därför naturen är full av regelbundna, matematiska mönster.
Fibonachos
Hittills har vi bara använt den rekursiva ekvationen för Fibonacci-nummer. Det finns faktiskt en uttrycklig ekvation också - men det är mycket svårare att hitta:
Vi kan också prova att välja olika utgångspunkter för Fibonacci-siffrorna. Om vi till exempel börjar med 2, 1, ... snarare än 1, 1, ... får vi en sekvens som heter Lucas-numren.
Det visar sig att oavsett två startnummer du väljer, de resulterande sekvenserna delar många egenskaper. Exempelvis kommer förhållandena mellan på varandra följande termer alltid
Det finns många andra pussel, mönster och applikationer relaterade till Fibonacci-nummer. Här är några exempel som du kan prova själv:
Problem solving
1. Fibonacci delbarhet
(a) Vilka Fibonacci-nummer är jämnt? Finns det ett mönster där de är placerade längs sekvensen? Kan du förklara varför?
(b) Vilka Fibonacci-nummer kan delas med 3 (eller delas med 4)? Vad märker du?
2. Fibonacci Sums
Vad händer om du lägger till tre Fibonacci-nummer i följd? Kan du förklara varför?
3. Fibonacci trappor
När jag går uppför trappan kan jag antingen ta enstaka steg eller hoppa över två steg åt gången. Det innebär att det finns många olika möjligheter för hur jag kan gå upp en trappa. Om det till exempel finns 5 steg har jag 8 olika val:
Hur många alternativ finns det för trappa med 6, 7 eller 8 steg? Kan du upptäcka ett mönster? Och hur är detta relaterat till Fibonacci-siffrorna?
© FoxTrot, by Bill Amend