Sekvenser och mönsterAritmetiska och geometriska sekvenser

1682 observerade astronomen Edmond Halley ett ovanligt fenomen: ett glödande vitt föremål med en lång svans som rörde sig över natthimlen. Det var en komet, en liten, isig sten som flyger genom rymden, medan han lämnar ett spår av damm och is.

Halley kom ihåg att andra astronomer hade observerat liknande kometer mycket tidigare: en 1530 och en annan 1606. Lägg märke till att klyftan mellan två på varandra följande observationer är densamma i båda fallen: år.

Image of Halley’s Comet,
taken in 1986 on Easter Island

Halley drog slutsatsen att alla tre observationerna i själva verket var av samma komet - som nu kallas Halleys komet. Den kretsar runt solen och passerar jorden ungefär vart 76 år. Han förutspådde också när kometen skulle bli synlig nästa:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

Faktiskt är tidsintervallet inte alltid exakt 76 år: det kan variera med ett eller två år, eftersom kometens bana avbryts av andra planeter. Idag vet vi att Halleys komet observerades av forntida astronomer redan 240 f.Kr.

Depections of Halley’s comet throughout time: a Babylonian tablet (164 BC), a medival tapestry (1070s), a science magazine (1910) and a Soviet stamp (1986).

En annan grupp forskare undersöker beteendet hos en studsande tennisboll. De tappade bollen från en höjd av 10 meter och mätte dess position över tid. Med varje studs förlorar bollen en del av sin ursprungliga höjd:

Forskarna märkte att bollen förlorar 20% av sin höjd efter varje studs. Med andra ord, den maximala höjden för varje studs är 80% av den föregående. Detta tillät dem att förutsäga höjden på varje följande studs:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

Definitioner

Om du jämför båda dessa problem, kanske du märker att det finns många likheter: sekvensen för Halleys komet har samma mellan på varandra följande termer, medan sekvensen av tennisbollsprång har samma [[-förhållande { 619} mellan på varandra följande villkor.

Sekvenser med dessa egenskaper har ett speciellt namn:

En aritmetisk sekvens har en konstant skillnad d mellan på varandra följande termer.

Samma nummer läggs till eller subtraheras för varje term för att producera nästa.

En geometrisk sekvens har ett konstant förhållande r mellan på varandra följande termer.

Varje term multipliceras eller delas med samma antal för att producera nästa.

Här är några olika sekvenser. Kan du bestämma vilka som är aritmetiska, geometriska eller varken, och vilka värden för d och r är?

2, 4, 8, 16, 32, 64, ...

är , med förhållandet .

2, 5, 8, 11, 14, 17, ...

är , med skillnad .

17, 13, 9, 5, 1, –3, ...

är , med skillnad .

2, 4, 7, 11, 16, 22, ...

är .

40, 20, 10, 5, 2,5, 1,25, ...

är , med förhållandet .

För att definiera en aritmetisk eller geometrisk sekvens måste vi veta inte bara den vanliga skillnaden eller förhållandet, utan också det initiala värdet (kallad a). Här kan du generera dina egna sekvenser och plotta deras värden på en graf genom att ändra värdena på a, d och r. Kan du hitta några mönster?

Aritmetisk sekvens

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Geometrisk sekvens

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Lägg märke till hur alla aritmetiska sekvenser ser väldigt lika ut: om skillnaden är positiv ökar de stadigt , och om skillnaden är negativ, minskar de stadigt .

Geometriska sekvenser kan å andra sidan bete sig helt annorlunda baserat på värdena på a och r:

Om kommer termerna , upp till oändlighet. Matematiker säger att sekvensen avviker.

Om kommer termerna alltid . Vi säger att sekvensen konvergerar.

Om , kommer termerna att växla mellan positivt och negativt, medan deras blir större.

Du lär dig mer om konvergens och avvikelse i sista avsnittet i den här kursen.

Rekursiva och explicita formler

I det föregående avsnittet fick du veta att en rekursiv formel berättar värdet för varje term som en funktion av tidigare termer. Här är de rekursiva formlerna för aritmetiska och geometriska sekvenser:

xn=

Ett problem med rekursiva formler är att för att hitta den 100: e termen, till exempel, måste vi först beräkna de tidigare 99 termerna - och det kan ta lång tid. Istället kan vi försöka hitta en uttrycklig formel, som säger värdet på n: e termen direkt.

För aritmetiska sekvenser måste vi lägga till d i varje steg:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

Vid n: e termen lägger vi till kopior av d, så den allmänna formeln är

xn=a+d×n−1.

För geometriska sekvenser måste vi multiplicera r vid varje steg:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

Vid n: e terminen multiplicerar vi kopior av r, så den allmänna formeln är

xn=a×rn−1.

Här är en sammanfattning av alla definitioner och formler som du hittills har sett:

En aritmetisk sekvens har första term a och gemensam skillnad d mellan på varandra följande termer.

Rekursiv formel: xn=xn−1+d

Explicit formel: xn=a+d×n−1

En geometrisk sekvens har första term a och gemensamt förhållande r mellan på varandra följande termer.

Rekursiv formel: xn=xn−1×r

Explicit formel: xn=a×rn−1

Låt oss nu titta på några exempel där vi kan använda allt detta!

Betala framåt

Här är ett kort klipp från filmen Pay it Forward, där 12-åriga Trevor förklarar sin idé för att göra världen till en bättre plats:

Kärnan i Trevors idé är att om alla ”betalar ut det” kan en enda person ha en enorm inverkan på världen:

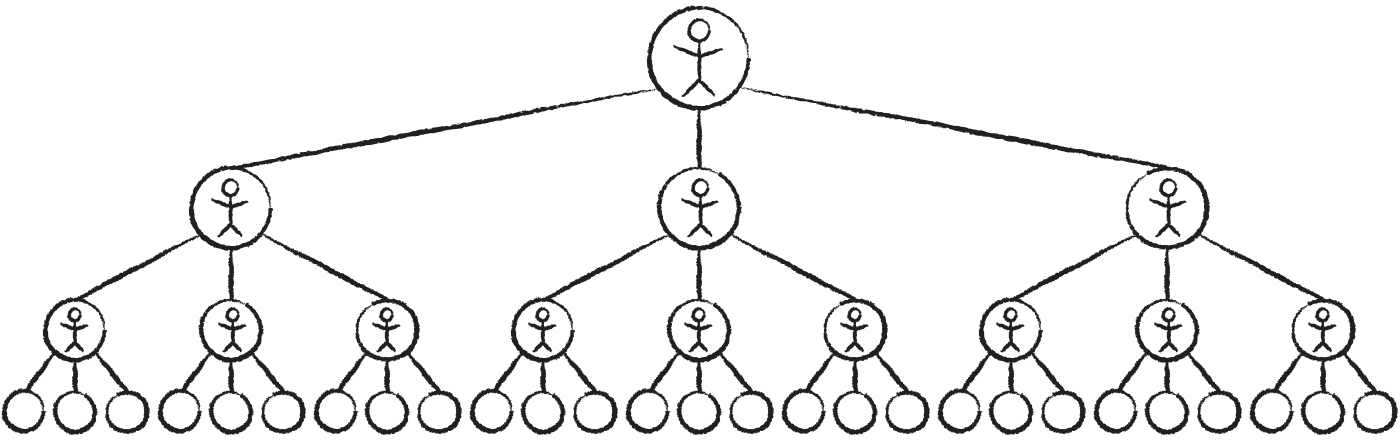
Lägg märke till hur antalet personer i varje steg bildar en , med gemensamt förhållande :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

Med hjälp av den explicita formeln för geometriska sekvenser kan vi ta reda på hur många nya människor som påverkas i vilket steg som helst:

xn =

Antalet människor ökar otroligt snabbt. På 10: e steget skulle du nå 19 683 nya, och efter 22 steg skulle du ha nått fler människor än som för närvarande lever på jorden.

Denna sekvens av siffror har ett speciellt namn: krafter på 3. Som ni ser är varje term faktiskt bara en annan effekt av 3:

30, 31, 32, 33, 34, 35, …

Vem vill bli miljonär?

KOMMER FÖR!

Chessboard-problemet

KOMMER FÖR!

Ändra språk

Logga in på Mathigon

Dela med sig

Återställ framsteg

Ordlista