Polygoner och polyhedraPlatoniska fasta partiklar

I början av denna kurs definierade vi vanliga polygoner som särskilt ”symmetriska” polygoner, där alla sidor och vinklar är desamma. Vi kan göra något liknande för polyeder.

I en vanlig polyhedron är alla ansikten alla samma typ av vanlig polygon, och samma antal ansikten möts vid varje toppunkt . Polyhedra med dessa två egenskaper kallas platoniska fasta ämnen , uppkallad efter den grekiska filosofen Platon .

Så hur ser de platoniska fasta ämnena ut - och hur många av dem finns det? För att göra en tredimensionell form, vi behöver minst ansikten för att möta vid varje vertex. Låt oss börja systematiskt med den minsta regelbundna polygonen: liksidiga trianglar:

Och sju eller flera trianglar i varje topp ger inte heller ny polyeder: det finns inte tillräckligt med utrymme runt en topp, för att passa så många trianglar.

Det betyder att vi har hittat platoniska fasta partiklar bestående av trianglar. Låt oss gå vidare till nästa vanliga polygon: rutor.

Låt oss sedan prova vanliga pentagoner:

Om pentagoner möts vid varje toppunkt, får vi Dodecahedron . Den har ansikten. ("Dodeca" betyder "tolv" på grekiska.)

Nästa regelbundna polygon att prova är hexagoner:

Om tre sexhörningar möts vid varje toppunkt får vi omedelbart en tessellation polyeder hexahedron . Eftersom det inte finns plats för mer än tre verkar det som om det inte finns några platoniska fasta partiklar som består av sexhörningar.

Detsamma gäller också för alla vanliga polygoner med mer än sex sidor. De tessellaterar inte, och vi får verkligen inga tredimensionella polygoner.

Detta innebär att det bara finns platoniska fasta ämnen! Låt oss titta på dem alla tillsammans:

Lägg märke till hur antalet ansikten och vertikaler byts runt densamma för kub och oktaeder , liksom dodekedron och icosahedron , medan antalet kanter förblir desamma är olika . Dessa par platoniska fasta material kallas dubbla fasta ämnen .

Vi kan förvandla en polyhedron till dess dubbla genom att "ersätta" varje ansikte med en topp och alla toppar med ett ansikte. Dessa animationer visar hur:

Tetraederen är dubbel med sig själv. Eftersom det har samma antal ansikten och toppar, byter du inte det skulle inte förändra någonting.

Platon trodde att all materia i universum består av fyra element: luft, jord, vatten och eld. Han trodde att varje element motsvarar ett av de platoniska fasta ämnena, medan det femte skulle representera universum som helhet. Idag vet vi att det finns mer än 100 olika element som består av sfäriska atomer, inte polyeder.

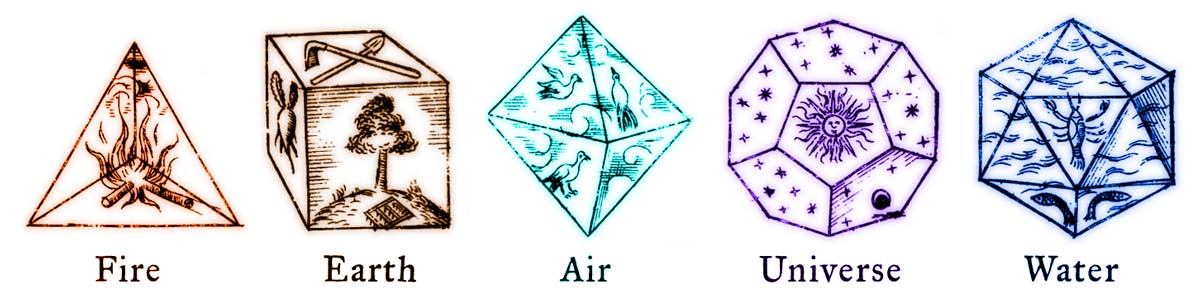
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)

Arkimediska fasta partiklar

Platoniska fasta ämnen är särskilt viktiga polyeder, men det finns otaliga andra.

Arkimediska fasta ämnen , till exempel, måste fortfarande bestå av vanliga polygoner , men du kan använda flera olika typer. De har fått sitt namn efter en annan grekisk matematiker, Archimedes of Syracuse , och det finns 13 av dem:

tillämpningar

Platon hade fel i att tro att alla element består av platoniska fasta ämnen. Men vanliga polyedrar har många speciella egenskaper som får dem att visas på andra håll i naturen - och vi kan kopiera dessa egenskaper inom vetenskap och teknik.