English
عربى
中文
Deutsch
Español
Français
हिन्दी
Hrvatski
Italiano
日本語
Português
Română
Русский
Svenska
Türkçe
Tiếng ViệtPolygoner och polyhedraTessellations
En polygon är geometrisk form som består av raka linjesegment. Polygoner kan inte innehålla några böjda sidor eller hål. Till exempel är en fyrkant en polygon men en cirkel är det inte. En tessellation är ett geometriskt mönster som täcker en yta utan mellanrum eller överlappningar.
Sinaloan Milk Snake skin
Cellstruktur av blad
Basaltkolonner på Giant's Causeway i Nordirland
Ananashud
Sköldpadda
Människor har kopierat många av dessa naturliga mönster inom konst, arkitektur och teknik - från antika Rom till nutid. Här är några exempel:
Växthus vid Eden-projektet i England
Mosaik i Alhambra
Cellulär tessellationspaviljong i Sydney
Studie av Regular Division of the Plane with Reptiles , MC Escher
Här kan du skapa dina egna tessellationer med vanliga polygoner. Dra helt enkelt nya former från sidofältet till duken. Vilka former stämmer väl? Finns det några former som inte tessellaterar alls? Försök skapa intressanta mönster!
Examples of other students’ tessellations
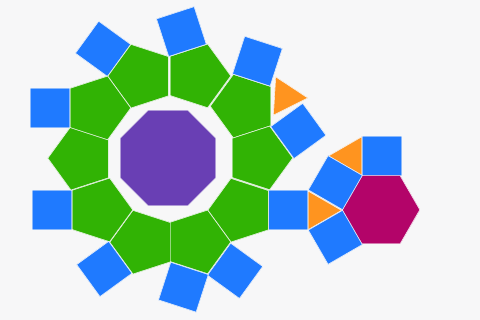
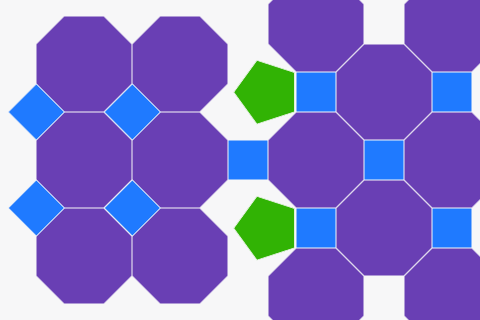
Tessellationer från vanliga polygoner
Du kanske har märkt att några En vanlig polygon är en polygon där alla sidor har samma längd och alla invändiga vinklar har samma storlek.
Detta har att göra med storleken på deras De inre vinklarna för en polygon är vinklarna på insidan, vid varje toppunkt. vertikaler för en polygon är de punkter där dess intilliggande sidor möts (dess "hörn").
Trianglar
Kvadrater
Pentagoner
Sexhörningar
Du kan på liknande sätt kontrollera att, precis som pentagoner, alla vanliga polygoner med sju eller fler sidor inte tessellaterar. Detta innebär att de enda vanliga polygonerna som tessellaterar är trianglar, rutor och hexagoner!
Naturligtvis kan man kombinera olika typer av vanliga polygoner i en tessellation, förutsatt att deras inre vinklar kan lägga till 360°:
Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°
Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°
Hexagons and triangles
120° + 120° + 60° + 60° = 360°
Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°
Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°
Octagons and squares
135° + 135° + 90° = 360°
Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°
Dodecagons, hexagons and squares
150° + 120° + 90° = 360°
Tessellationer från oregelbundna polygoner
Vi kan också prova att göra tessellationer av En oregelbunden polygon är en som är inte vanlig. Det betyder att antingen sidorna eller vinklarna inte alla har samma storlek.
Det visar sig att du kan tessellera inte bara liksidiga trianglar, utan vilken triangel som helst ! Försök att flytta topparna i detta diagram.
Summan av de inre vinklarna i en triangel är
Mer överraskande, alla fyrkantiga tessellater också! Deras inre vinkelsumma är
Pentagoner är lite svårare. Vi såg redan att vanliga pentagoner
Här är tre olika exempel på tessellationer med pentagoner. De är inte vanliga , men de är giltiga 5-sidiga polygoner.
Hittills har matematiker bara hittat 15 olika typer av tessellationer med (konvexa) pentagoner - den senaste upptäcktes 2015. Ingen vet om det finns några andra, eller om dessa 15 är de enda ...
Tessellationer i art
Tessellations vi både ett verktyg och inspiration för många konstnärer, arkitekter och designer - mest känd den holländska konstnären Maurits Cornelis Escher (1898 - 1972) var en holländsk konstnär som skapade skisser, träsnitt och litografier av matematiskt inspirerade föremål och former: inklusive polyhedra, tessellationer och omöjliga former. Han utforskade grafiskt begrepp som symmetri, oändlighet, perspektiv och icke-euklidisk geometri.
“Sky and Water I” (1938)
“Lizard” (1942)
“Lizard, Fish, Bat” (1952)
“Butterfly” (1948)
“Two Fish” (1942)
“Shells and Starfish” (1941)
Dessa konstverk ser ofta roliga och enkla ut, men de underliggande matematiska principerna är desamma som tidigare: vinklar, rotationer, översättningar och polygoner. Om matematiken inte är rätt kommer tessellationen inte att fungera!
“Metamorphosis II” by M. C. Escher (1940)
Penrose brickor
Alla tessellationer vi såg hittills har en sak gemensamt: de är periodiska . Det betyder att de består av ett regelbundet mönster som upprepas om och om igen. De kan fortsätta för evigt i alla riktningar och de kommer att se lika ut överallt.
På 1970-talet upptäckte den brittiska matematikern och fysikern Sir Roger Penrose (född 1931) är en brittisk matematiker och fysiker som är känd för sitt banbrytande arbete inom allmän relativitet och kosmologi - ofta i samarbete med andra berömda forskare som Stephen Hawking och Michael Atiyah. Han upptäckte också Penrose Tilings: självliknande, icke-periodiska tessellationer.
Move the slider to reveal the underlying structure of this tessellation. Notice how you have the same patterns at various scales: the small yellow pentagons, blue stars, orange rhombi and green ‘ships’ appear in their original size, in a slightly larger size and an even larger size. This self-similarity can be used to prove that this Penrose tiling is non-periodic.
Penrose utforskade tessellationerna bara för skojs skull, men det visar sig att den inre strukturen i vissa verkliga material (som aluminium) följer ett liknande mönster. Mönstret användes till och med på toalettpapper, eftersom tillverkarna märkte att ett icke-periodiskt mönster kan rullas upp utan utbuktningar.