Transformationer och symmetriSymmetri grupper och bakgrundsbilder
Vissa former har mer än en symmetri - låt oss titta på








Du har redan visat ovan att en fyrkant har
Den har också rotationssymmetri med
Och slutligen kan vi tänka på att ”göra ingenting” som en annan speciell typ av symmetri - för resultatet är (uppenbarligen) detsamma som tidigare. Detta kallas ibland identiteten .
Totalt har vi hittat
Nu kan vi faktiskt börja göra lite aritmetik med dessa symmetrier. Vi kan till exempel lägga till två symmetrier för att få nya:






När du lägger till två symmetrier på en kvadrat får du en ny. Här är en "symmetriskräknare" där du kan prova själv:
Spendera lite tid med att leka med symmeträknaren och försök hitta mönster. Kan du slutföra dessa observationer?
- Att lägga till två rotationer ger alltid
(eller identiteten). * Att lägga till två reflektioner ger alltid (eller identiteten). * Att lägga till samma två symmetrier i motsatt ordning resultat. * Att lägga till identiteten .
Du kanske redan har insett att lägga till symmetrier liknar faktiskt mycket att lägga till heltal :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
I matematik kallas varje samling som har dessa egenskaper en
I det här exemplet började vi med de åtta symmetrierna på torget. Faktum är att varje geometrisk form har sin egen symmetergrupp . De har alla olika element, men de uppfyller alltid de tre reglerna ovan.
Grupper visas överallt i matematik. Elementen kan vara siffror eller symmetrier, men också polynomier, permutationer, matriser, funktioner ... allt som följer de tre reglerna. Den centrala idén med gruppteori är att vi inte är intresserade av de enskilda elementen, bara i hur de interagerar med varandra .
Exempelvis kan symmeturgrupperna för olika molekyler hjälpa forskare att förutsäga och förklara egenskaperna hos motsvarande material.
Grupper kan också användas för att analysera den vinnande strategin i brädspel, uppförandet av virus i medicin, olika harmonier i musik och många andra begrepp ...
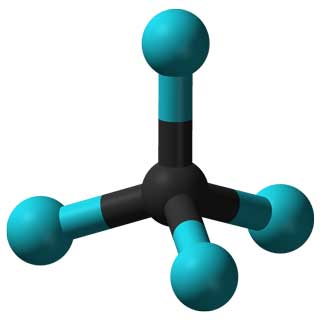
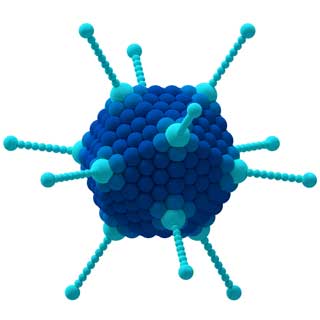
Egenskaperna hos den CCl 4-molekylen (vänster) och Adenovirus (höger) bestäms av deras symmetrier.
Tapetgrupper
I de föregående avsnitten såg vi två olika slags symmetri motsvarande två olika transformationer: rotationer och reflektioner. Men det finns också en symmetri för den tredje typen av styv transformation:


Hexagonal honyecomb


Keramisk väggbeläggning
Förutom reflektions-, rotations- och translationssymmetri finns det till och med en fjärde typ:


Ett mönster kan ha mer än en typ av symmetri. Och precis som för rutor kan vi hitta
Dessa grupper berättar inte så mycket om hur mönstret ser ut (t.ex. dess färger och former), bara hur det upprepas . Flera olika mönster kan ha samma symmeturgrupp - så länge är ordnade och upprepade på samma sätt.


Dessa två mönster har samma symmetrier, även om de ser väldigt olika ut. Men symmetrier handlar inte om färger eller ytliga former.


Dessa två mönster har också samma symmetrier - även om de ser mer ut som motsvarande mönster till vänster än varandra.
Det visar sig att även om det finns oändligt många möjliga mönster har de alla en av bara 17 olika symmeturgrupper. Dessa kallas tapetgrupper . Varje tapetgrupp definieras av en kombination av översättningar, rotationer, reflektioner och glidreflektioner. Kan du se

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
Tyvärr finns det ingen enkel anledning till att det finns 17 av dessa grupper, och för att bevisa att det kräver mer avancerad matematik. Istället kan du prova att rita dina egna upprepade mönster för var och en av de 17 tapetgrupperna:
Examples of other students’ drawings



Tapetgrupperna handlade om platta, tvådimensionella mönster. Vi kan göra något liknande för tredimensionella mönster: dessa kallas kristallografiska grupper, och det finns 219 av dem!
Förutom översättningar, reflektioner, rotationer och glidreflektioner inkluderar dessa grupper symmetrier som glidplan och skruvaxlar (tänk på rörelsen när du skruvar av en flaska).
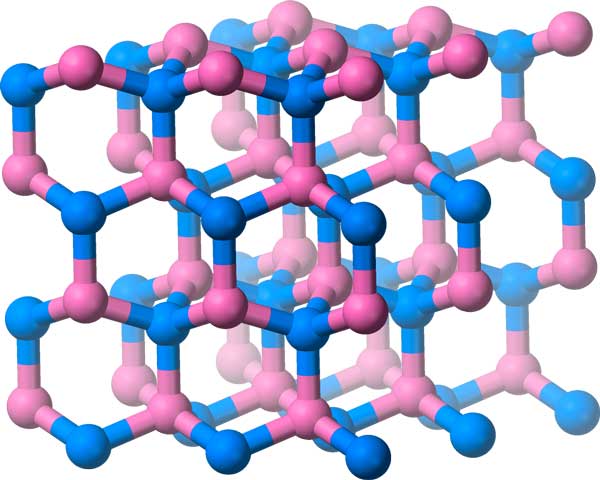
Boron-nitrid har sina molekyler arrangerade i detta kristallgitter, som har en tredimensionell symmeturgrupp.