FraktalerMandelbrot-uppsättningen

Alla fraktaler som vi såg i de föregående kapitlen skapades med en process med iteration: du börjar med ett specifikt mönster och sedan upprepar det om och om igen.

Detta liknar ett annat begrepp i matematik som du såg tidigare: med rekursiva sekvenser börjar du med ett specifikt nummer, och sedan använder du samma rekursiva formel, om och om igen, för att få nästa nummer i sekvens.

Låt oss ta den rekursiva formeln xn=xn−12 som ett exempel och plotta dess termer på en siffra. Du kan ändra värdet på x0:

Lägg märke till hur den resulterande sekvensen kan bete sig mycket annorlunda beroende på startvärdet x0:

Hittills har vi inte lärt oss något nytt. Men för ungefär ett århundrade sedan började matematiker att utforska vad som händer med dessa sekvenser om du använder komplexa siffror, snarare än bara den verkliga talraden. Deras upptäckter var några av de mest överraskande och vackraste resultaten i all matematik.

Julia Sets

Låt oss använda samma sekvens som tidigare, xn=xn−12, men på det komplexa planet. Du kan flytta positionen för x0 för att se vad som händer med följande termer. Om sekvensen ser ut som om den kommer att gå samman, låt oss färga motsvarande punkt på planet i blå:

Som ni ser konvergerar sekvensen så länge x0 ligger inuti enhetscirkeln outside the unit squareabove the >>>>x<<<<-axis (cirkeln med radien 1, centrerad vid ursprunget).

Låt oss nu göra saker lite svårare. Istället för att bara kvadratera det föregående talet lägger vi också till en konstant c varje gång (vilket kan vara vilket komplex nummer som helst). Med andra ord, xn=xn−12+c. Tror du att vi fortfarande får en cirkel av konvergens? Vilka andra former tror du att vi kan se? Fortsätt

I detta diagram kan du flytta positionen för x0 såväl som värdet på c:

De olika formerna som bildas genom färgning i siffrorna kallas Julia Sets. De upptäcktes oberoende av två franska matematiker, Gaston Julia och Pierre Fatou, omkring 1918.

På den tiden fanns det inga datorer som hjälpte till att visualisera hur Julia-uppsättningarna faktiskt såg ut. Matematiker som Julia och Fatou kunde resonera om dem matematiskt, men de såg någonsin bara grova, handritade skisser av hur de kan se ut.

Vi har inte det här problemet idag - bilderna nedan är alla av olika Julia-uppsättningar. De olika färgerna indikerar hur snabbt sekvensen vid den punkten avviker:

Fortsätt

Mandelbrot-uppsättningen

När du skapar de olika Julia-uppsättningarna kanske du har lagt märke till att det fanns några värden på c som varje sekvens avviker från och hela komplexa planet förblir vitt. Några decennier efter Julia och Fatou försökte en ny generation matematiker att kartlägga hur dessa områden såg ut.

I föregående exempel valde vi ett fast värde för c och ändrade sedan positionen för x0 för att färga planet. Låt oss nu fixa värdet på x0=0 och ändra istället värdet på c.

Återigen måla du över det komplexa planet för att avslöja området där sekvenserna förblir avgränsade. Vilka former förväntar du dig att dyka upp?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Denna fraktal kallas Mandelbrot Set, och när den roteras 90 ° ser den nästan ut som en person, med huvud, kropp och två armar. Det definierades och ritades för första gången 1978 i ett forskningsdokument av matematikerna Robert Brooks och Peter Matelski:

Några år senare använde Benoit Mandelbrot de kraftfulla datorerna hos IBM för att skapa en mycket mer detaljerad visualisering av fraktalen, som senare fick sitt namn efter honom. De första utskrifterna såg annorlunda ut än vad han förväntade sig - tills han insåg att teknikerna som arbetade på skrivarna städade upp "fuzziness" runt dess kant, med antagande att det orsakades av dammpartiklar eller skrivarfel och inte ett definierande kännetecken för fraktaler ! Fortsätt

Liksom alla fraktaler kan vi "zooma in" i Mandelbrot-set för alltid och hitta nya mönster i varje skala. Här kan du zooma in på en del av Mandelbrot-uppsättningen som kallas Seahorse Valley. Svarta punkter är inuti Mandelbrot-uppsättningen, där sekvensen är begränsad. Färgade punkter är utanför Mandelbrot-uppsättningen, där sekvensen avviker, och de olika färgerna indikerar hur snabbt den växer till oändlighet:

Scale: ${pow(scale)}

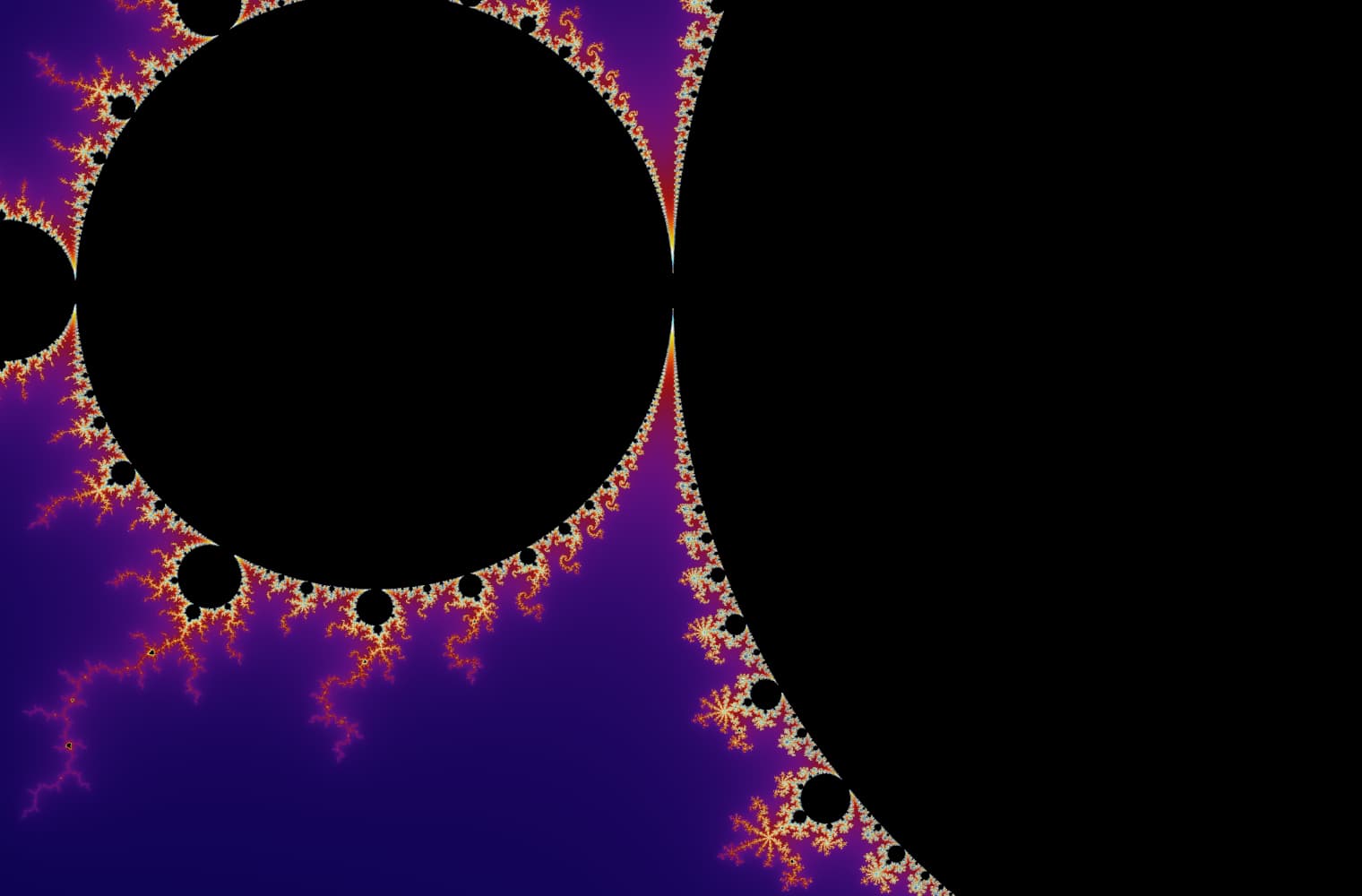
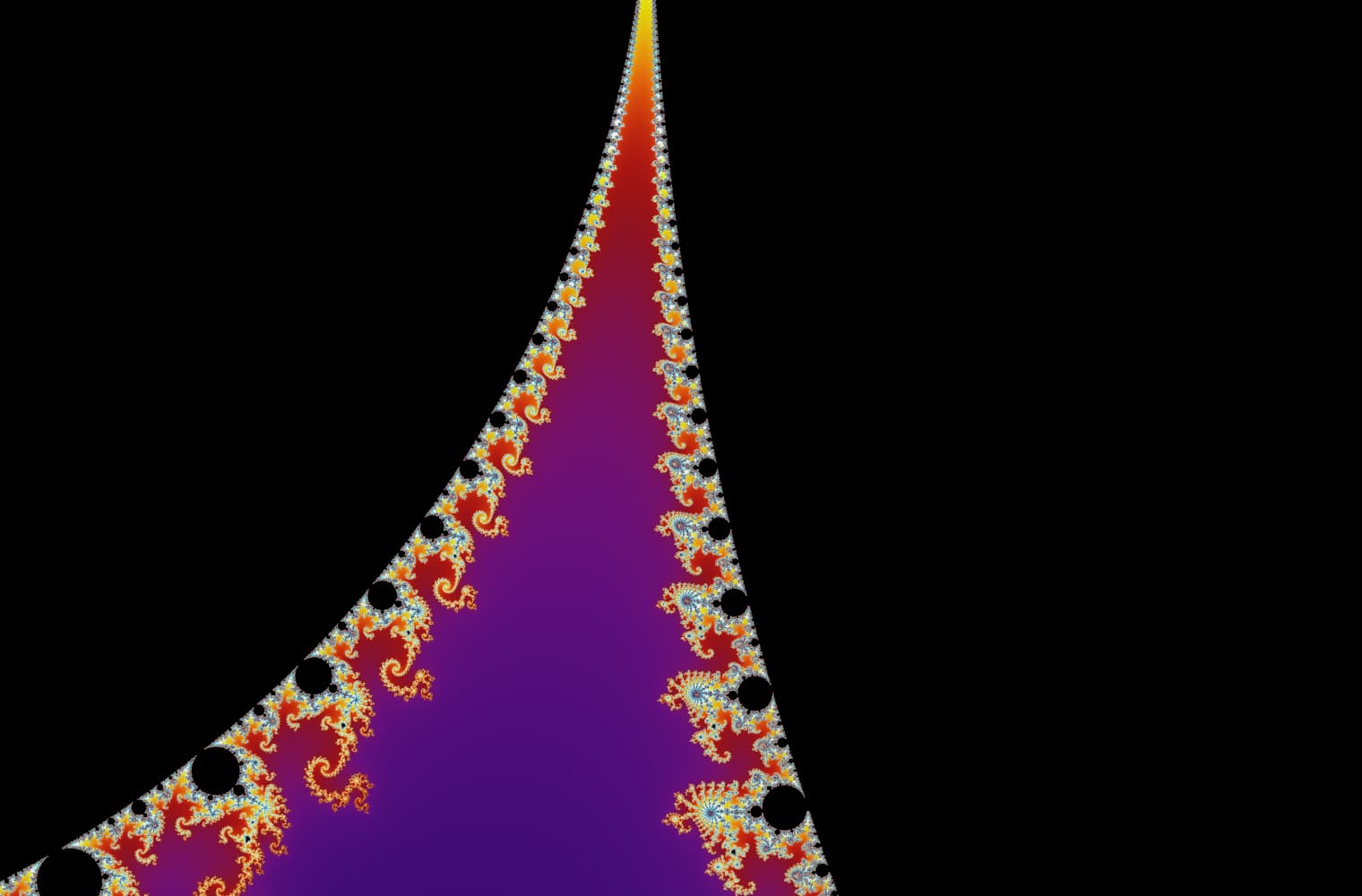
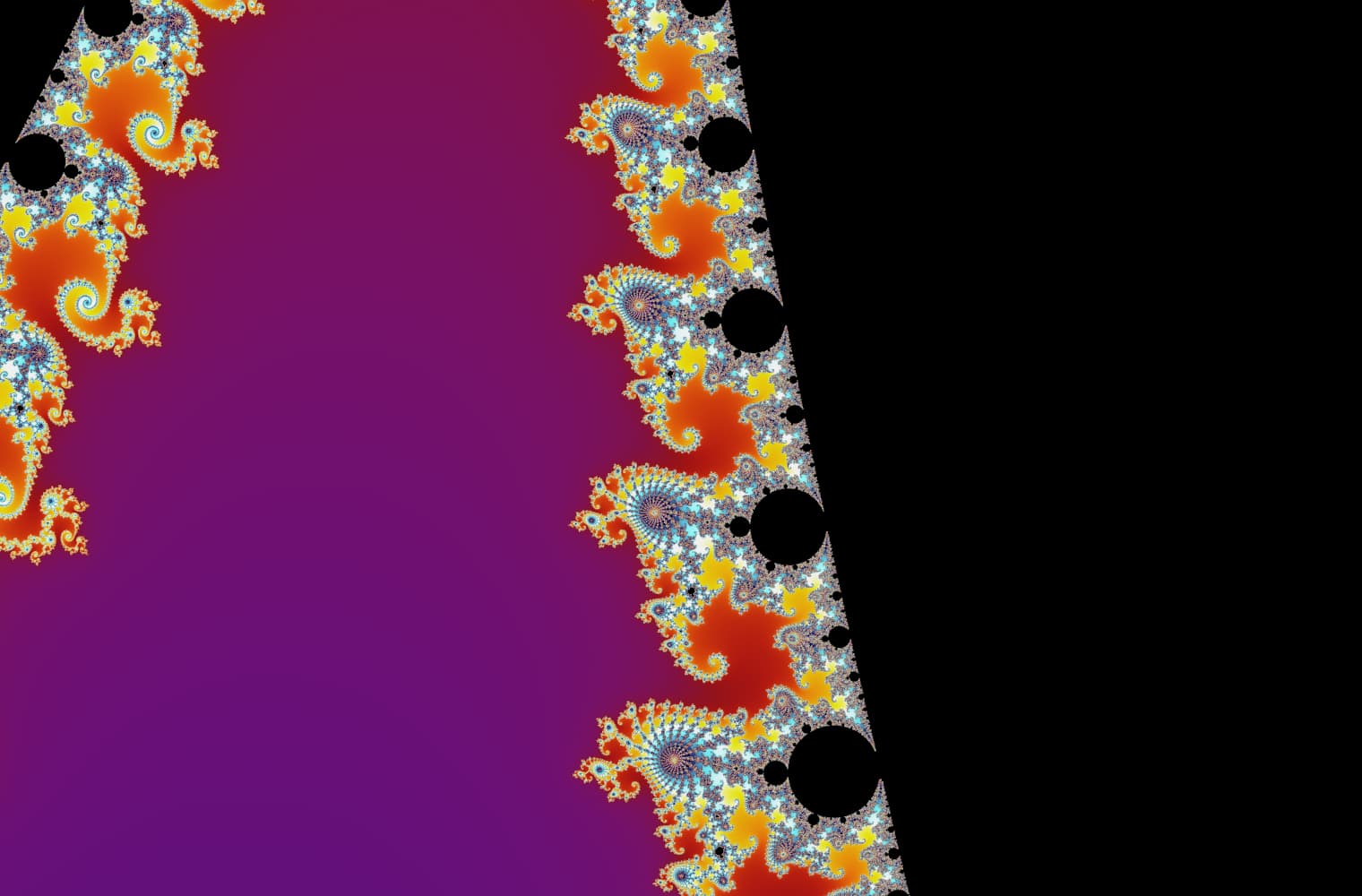
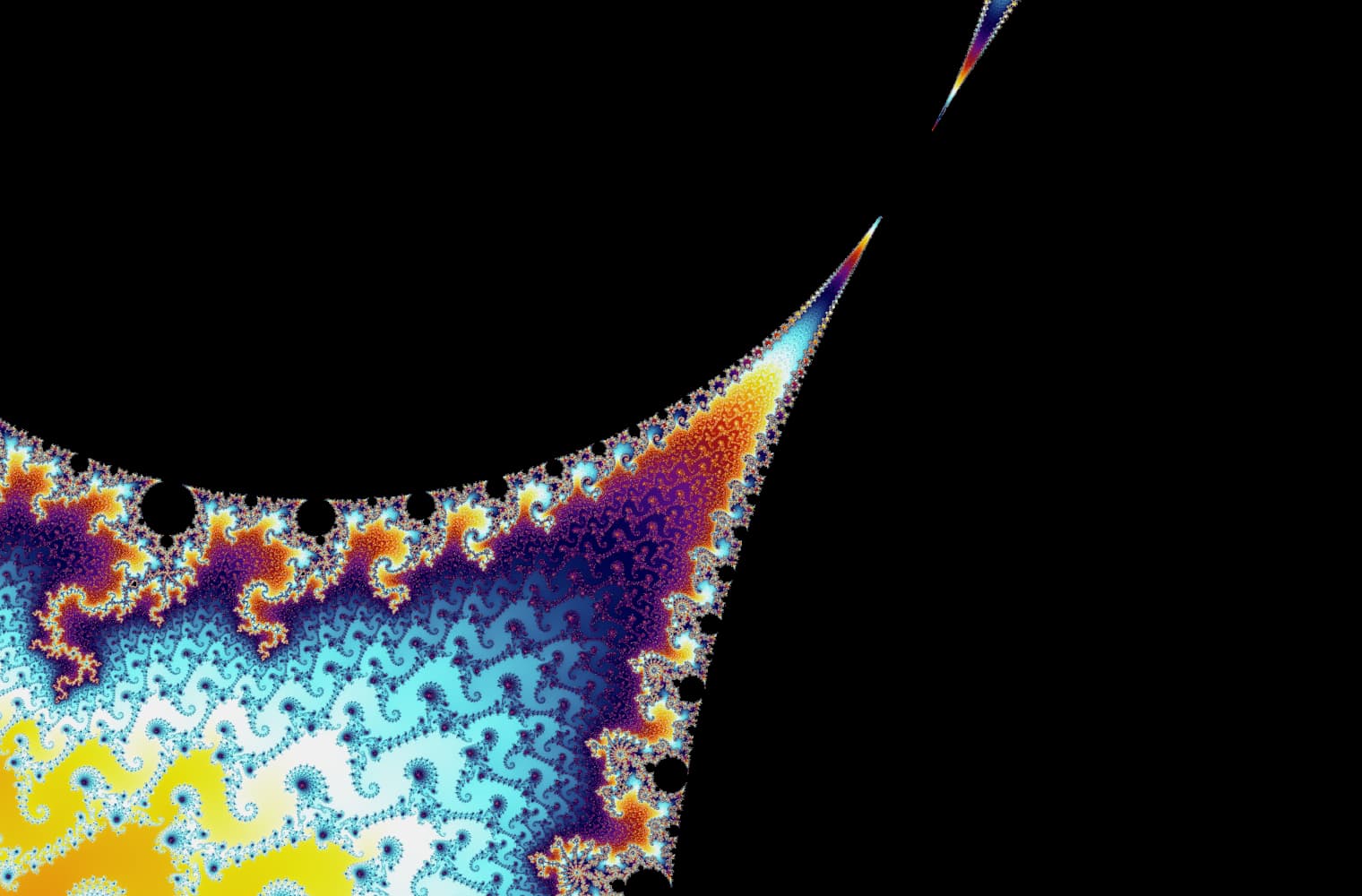
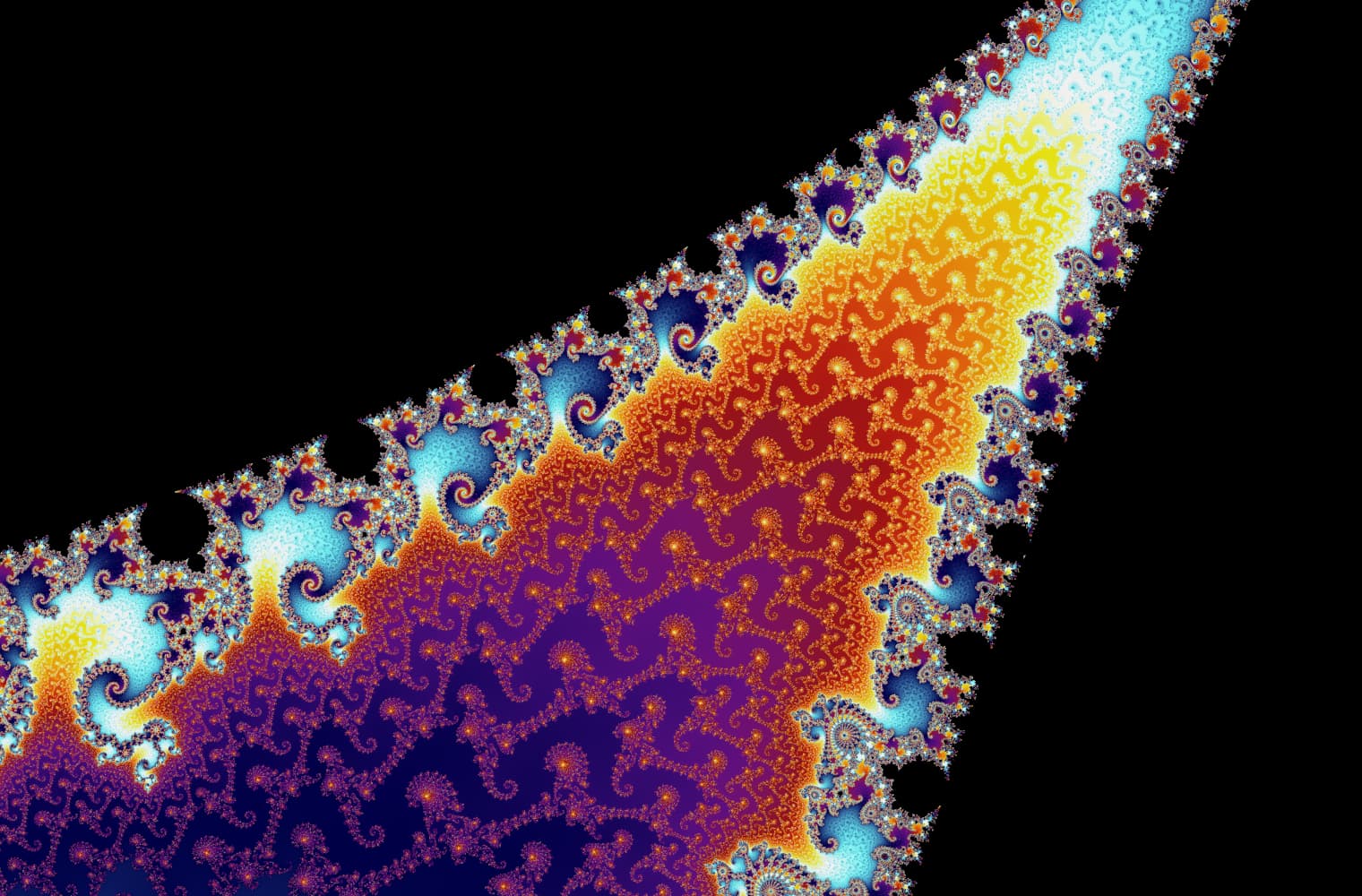
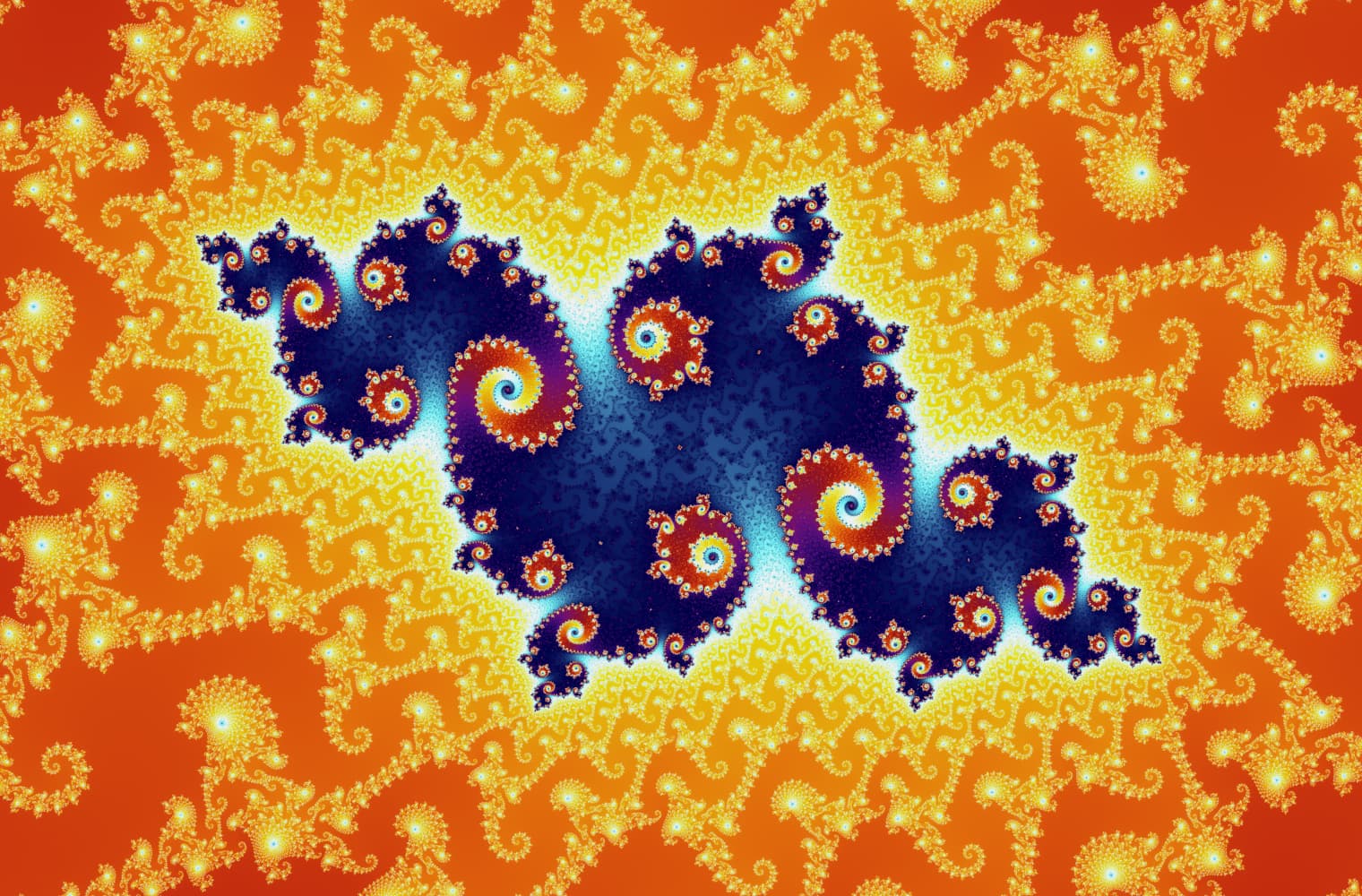
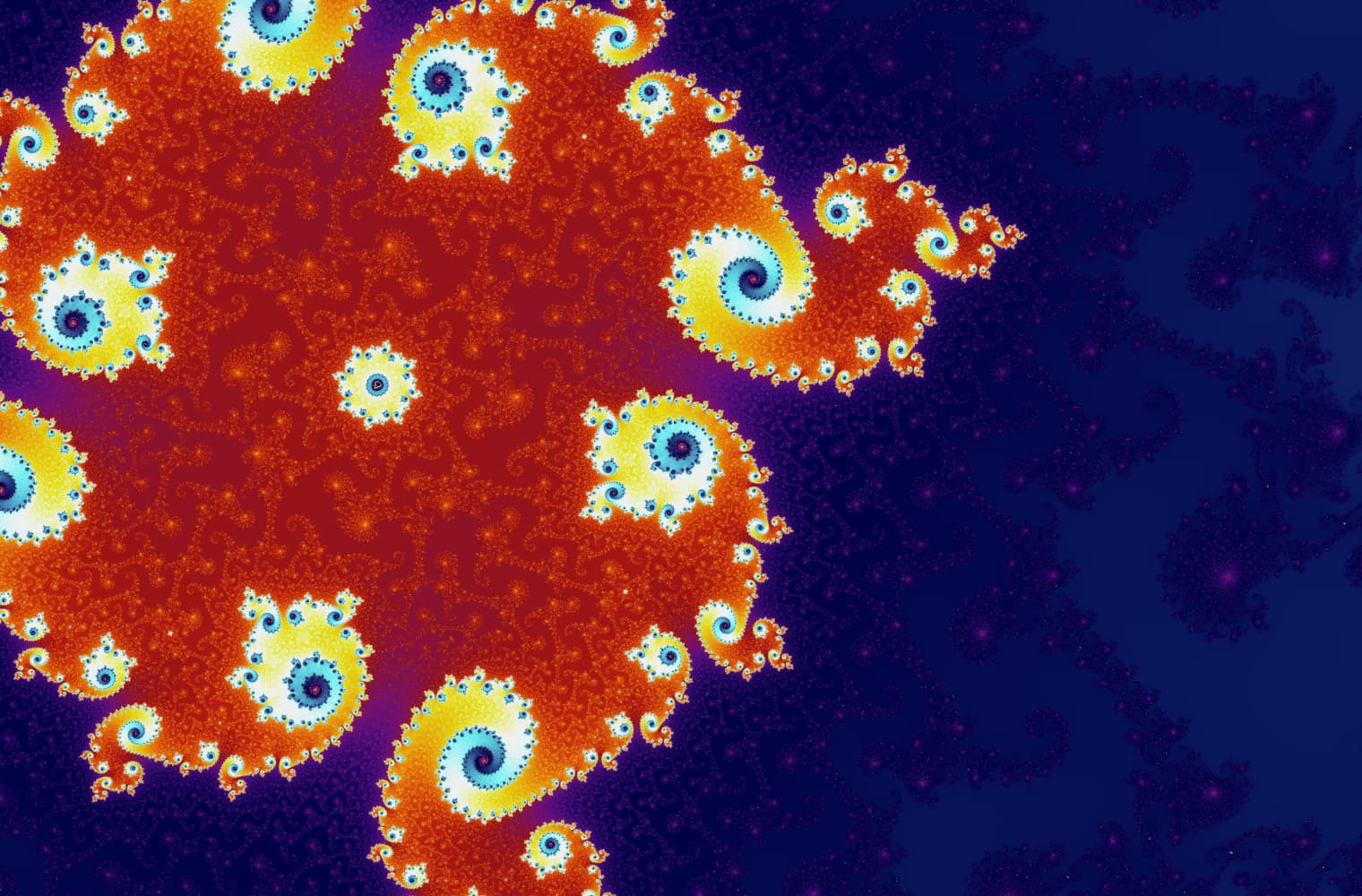
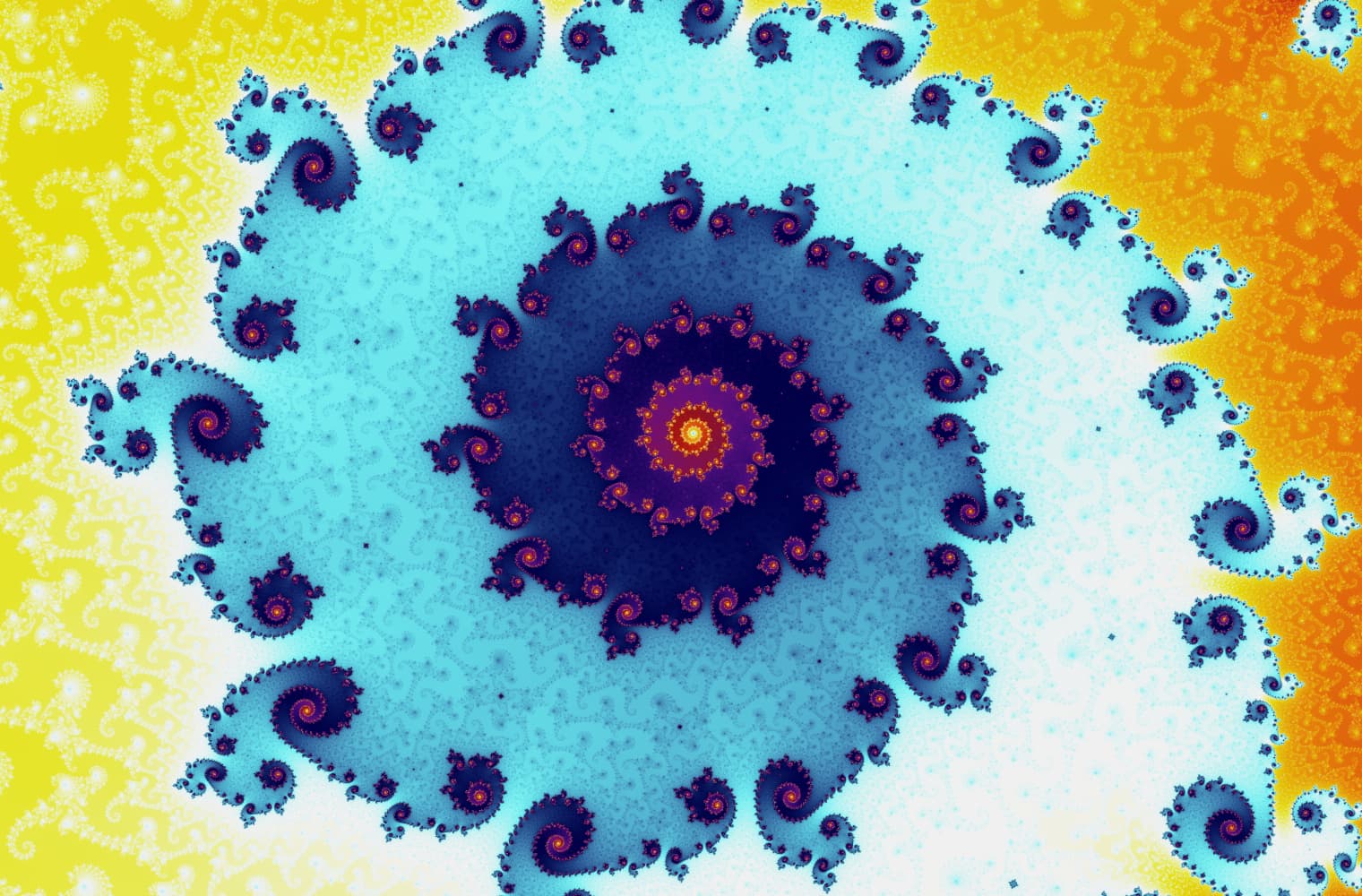
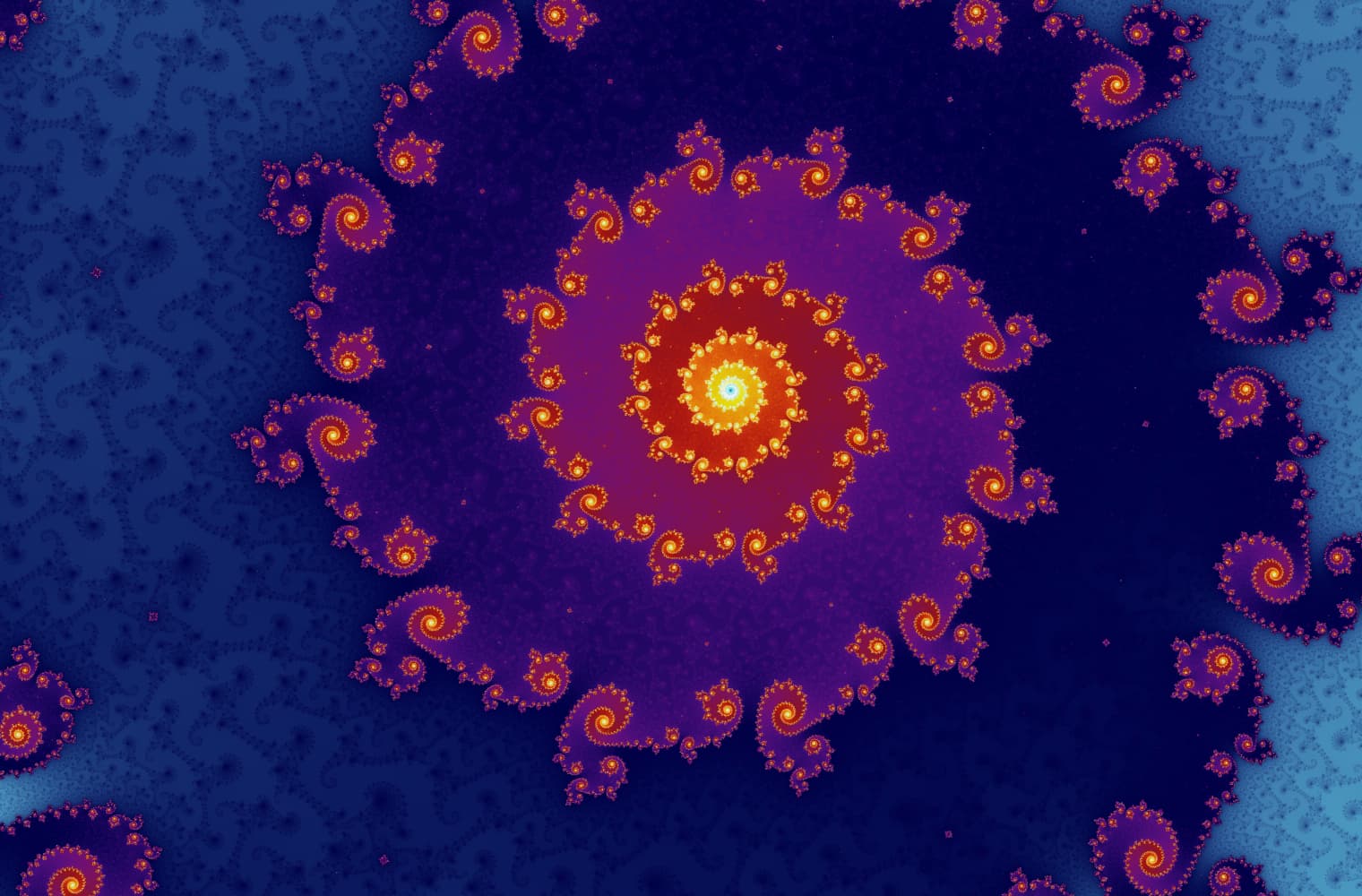
Denna skjutreglage består av 27 enskilda bilder, upp till en zoomnivå på över 14 kvadrillioner, eller 254. Sammantaget tog de nästan 45 minuter att rendera på en modern bärbar dator. Mandelbrot-uppsättningen kan skapas med bara en enda enkel ekvation xn=xn−12+c, men den är oändligt komplex och otroligt vacker.

När du flyttar värdet på c runt Mandelbrot-uppsättningen kanske du märker en nyfiken egenskap:

• Alla sekvenser inom huvudkroppen av Mandelbrot-uppsättningen konvergerardivergereach an orbit till en enda punkt.
• Sekvenserna i den stora lampan överst når en banaconvergediverge som består av poäng.
• Sekvenser i denna mindre glödlampa har banor med längden .

Varje glödlampa har en bana i olika storlekar, med mindre glödlampor med fler och fler punkter i sina banor. Storleken på dessa banor är nära besläktade med Logistic Map, ett viktigt begrepp i Chaos theory.