FraktalerIntroduktion
När du tittar runt naturen kanske du har märkt intrikata växter som dessa:


Denna Fern består av många små blad som grenar bort en större.


Denna Romanesco broccoli består av mindre
Ursprungligen verkar dessa vara mycket komplexa former - men när du tittar närmare kanske du märker att de båda följer ett relativt enkelt mönster: alla enskilda delar av växterna ser exakt lika ut som hela växt, bara mindre. Samma mönster upprepas om och om igen, i mindre skalor.
I matematik kallar vi den här egenskapen självlikhet, och former som har den kallas
För att skapa våra egna fraktaler måste vi börja med ett enkelt mönster och sedan upprepa det om och om igen, i mindre skalor.
Ett av de enklaste mönstren kan vara ett radsegment, med ytterligare två segment som förgrenas ena änden. Om vi upprepar detta mönster kommer båda dessa blå segment också att ha ytterligare två grenar i sina ändar.
Du kan flytta blå prickar för att ändra längden och vinkeln på alla grenarna. Öka sedan antalet iterationer med
Beroende på grenarnas placering kan du göra helt olika mönster - ser ut som ovan, ett eller . Vad hittar du mer?
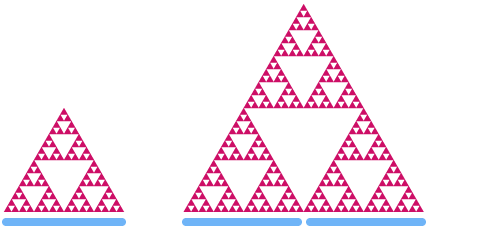
En annan berömd fraktal är
Lägg märke till hur den slutliga formen består av tre identiska kopior av sig själv, och var och en av dessa består av ännu mindre kopior av hela triangeln! Du kan fortsätta zooma in i triangeln för alltid, och mönstren och formerna kommer alltid att upprepa.
Växterna i början av detta kapitel ser precis som fraktaler, men det är helt klart omöjligt att skapa verkliga fraktaler i verkligheten. Om vi fortsätter att upprepa samma mönster om och om igen, mindre och mindre, skulle vi så småningom komma till celler, molekyler eller atomer som inte längre kan delas upp.
Men med matematik kan vi tänka på de egenskaper som verkliga fraktaler "skulle" ha - och dessa är mycket överraskande ...
Fraktala dimensioner
Låt oss först tänka på fraktalernas dimension. En rad har dimension
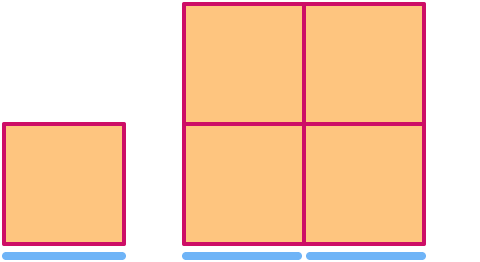
En kvadrat har dimension
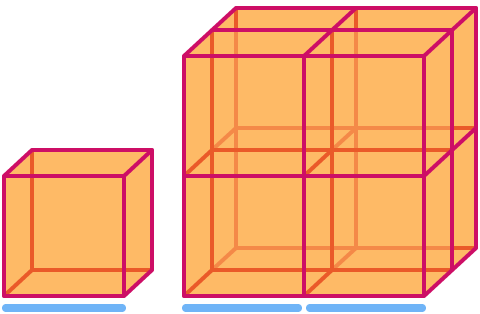
En kub har dimensionen
Låt oss titta på Sierpinski-triangeln. Om vi skalar det med en faktor 2, kan du se att det är "area" ökar med en faktor på
Låt oss säga att d är dimensionen i Sierpinski-triangeln. Med samma mönster som ovan får vi
Men vänta ... hur kan något ha en dimension som inte är ett heltal? Det verkar omöjligt, men detta är bara en av de konstiga egenskaperna hos fraktaler. I själva verket är det detta som ger fraktaler deras namn: de har en fraktionerad dimension.
Med varje iteration tar vi bort en del av Sierpinski-triangeln. Om vi kunde göra detta oändligt många gånger, skulle det faktiskt inte finnas något område kvar: det är därför Sierpinski-triangeln är något mellan ett tvådimensionellt område och en 1-dimensionell linje.
Medan många fraktaler är självliknande, är en bättre definition att fraktaler är former som har en icke-heltal-dimension.
The Koch Snowflake
Det finns många former i naturen som ser ut som fraktaler. Vi har redan sett några växter i början av detta kapitel. Andra bra exempel är snöflingor och iskristaller:
För att skapa vår egen fraktal snöflinga måste vi återigen hitta en enkel procedur vi kan använda om och om igen.
Liksom Sierpinski-triangeln, låt oss börja med en enda, liksidig triangel. I stället för att ta bort mindre trianglar i varje steg, lägger vi till mindre trianglar längs kanten. Sidolängden för varje triangel är
Den resulterande formen kallas
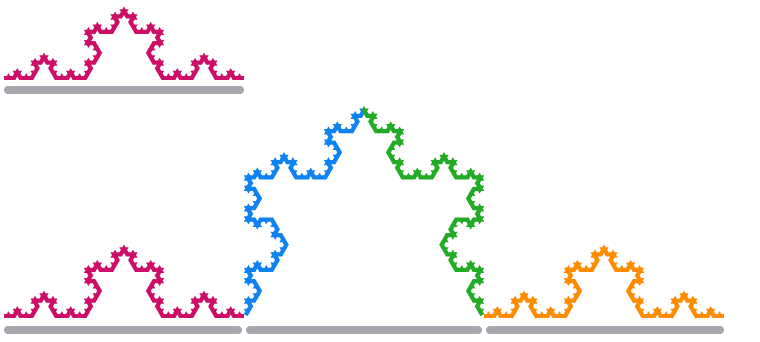
När vi skalar ett kantsegment av Koch Snowflake med en faktor 3, är dess längd
Med samma förhållande mellan dimensioner och skalfaktorer som ovan får vi ekvationen
Område
Att skapa Koch-snöflingor är nästan som en




Efter den första iterationen ökar antalet nya trianglar som läggs till med en faktor
Låt oss säga att
Med hjälp av formeln för summan av oändliga
Omkrets
Vi kan också försöka beräkna Koch-snöflingans omkrets. Som vi redan har sett förändras omkretsens längd med en faktor
Det betyder att vi ännu en gång har en geometrisk serie - men i detta fall konvergerar den

Om detta verkar motsatt, kom bara ihåg att vi multiplicerar omkretsen med
Det är nästan otänkbart att du kan ha en form med ett ändligt område och också en oändlig omkrets - men detta är bara en av de många oväntade egenskaperna hos fraktaler.
Kan du hitta några andra sätt att skapa dina egna fraktaler?
"Min själ spiralerar på frysta fraktaler runt ..."
Menger Sponge
Fraktaler behöver inte vara "platta", som många av exemplen ovan. En av de mest kända fraktaler som ser tredimensionell ut är Menger-svamp, uppkallad efter matematikern
Vi börjar med en solid kub och borrar upprepade gånger mindre och mindre hål i sidorna. Varje ny iteration av hål har
En
Nu kan vi försöka beräkna dimensionen d på Menger-svampen precis som vi gjorde för Kochs snöflinga ovan. I det här fallet får vi
Om du föreställer dig att skära ut fler och fler hål, oändligt många gånger, skulle det inte finnas någon faktisk volym kvar. Det är därför kuben är "inte riktigt" tredimensionell!
Fraktkustlinjer
En av de viktigaste egenskaperna för alla fraktaler som vi hittills har sett är att du kan "zooma in" för alltid och alltid hitta nya mönster. Cirka 1920 insåg den brittiska matematikern
Du börjar med landets grundform, och när du zooma in lägger du till flodinlopp, vikar och flodmynningar, sedan enskilda klippor, klippor, stenar och så vidare:
Detta är ett betydande problem när du försöker beräkna längden på landets gräns - hur bestämmer du hur långt du vill zooma in och vilka krök och krokar du vill inkludera?
Ett sätt vi kan mäta längden på Storbritanniens kust, till exempel, är att ta en lång linjal, gå hela vägen runt dess stränder och sedan lägga till alla avstånd.
Om linjalen är
Vi kan bara fortsätta, med mindre och mindre linjaler, och varje gång vårt resultat för kustlinjens längd skulle bli lite längre. Precis som Koch Snowflake tidigare verkar det som om Storbritanniens kustlinje är oändligt lång! Detta kallas ofta kustlinjeparadox.
Några decennier senare snubblade matematikern
Storbritanniens kustlinje "ser" visserligen ut fraktalen, men den är inte självliknande, som andra fraktaler som vi har sett tidigare. För att hitta dess storlek kan vi rita det på ett rutnät och räkna antalet celler som det korsar varandra.
Till att börja med finns det 88 korsande celler. Om vi skalar kustlinjen med en faktor 2, finns 197 korsande celler - mer än dubbelt så många!
Storleken på kustlinjen har ökat med en faktor
Om vi upprepar detta med större rutnät hittar vi att dimensionen av Storbritanniens kustlinje faktiskt är ungefär 1,21. Mandelbrot insåg att denna fraktala dimension också är ett mått på råhet av en form - ett nytt koncept, för vilket han fann viktiga tillämpningar inom många andra områden inom matematik och naturvetenskap.
Fler fraktaler inom natur och teknik
Även om sanna fraktaler aldrig kan visas i naturen, finns det många objekt som ser nästan ut som fraktaler. Vi har redan sett växter, snöflingor och kustlinjer, och här är några fler exempel:
Bergskedja i centrala Asien
Ganges floddelta i Indien
Blixtbultar
Blodkärl i näthinnan
Grand Canyon i USA
Moln
Alla dessa objekt kan verka helt slumpmässiga, men precis som fraktaler finns det ett underliggande mönster som avgör hur de bildas. Matematik kan hjälpa oss att förstå formerna bättre, och fraktaler har tillämpningar inom områden som medicin, biologi, geologi och meteorologi.
Datorgenererad fraktal terräng
Vi kan också använda fraktaler för att skapa realistiska "kopior" av naturen, till exempel som landskap och texturer som används i videospel eller datorgenererade filmer. Vattnet, bergen och molnen i denna bild tillverkas helt av en dator med hjälp av fraktaler!
Och vi kan till och med vända den här processen för att komprimera digitala bilder för att minska deras filstorlek. De första algoritmerna utvecklades av Michael Barnsley och Alan Sloan på 1980-talet och nya undersöks fortfarande idag.